Сетка визуализированная с ограничивающей
Рисунок 11.4. Сетка визуализированная с ограничивающей сферой и ограничивающим параллелепипедом. Сфера определяется путем задания центральной точки и радиуса. Параллелепипед определяется путем задания двух углов
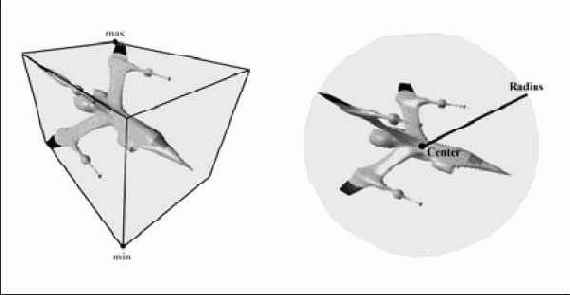
Ограничивающие параллелепипеды и сферы, помимо прочего, часто используются для быстрой проверки видимости объектов и для обнаружения столкновений. Например, если не видна ограничивающая сфера или ограничивающий параллелепипед сетки, значит не видна и сама сетка. Проверка видимости сферы или параллелепипеда выполняется гораздо быстрее, чем проверка видимости каждого треугольника сетки. Что касается обнаружения столкновений, предположим, что в сцене выпущена ракета и нам необходимо определить, столкнулась ли она с каким-нибудь объектом сцены. Поскольку объекты состоят из треугольных граней, нам надо перебрать каждую грань каждого объекта и проверить столкнулась ли с ней ракета (которая математически моделируется с помощью луча). Этот подход требует огромного количества проверок пересечения луча с треугольником — по одной проверке для каждой грани каждого объекта сцены. Более эффективный подход заключается в вычислении для каждой сетки ограничивающей сферы или ограничивающего параллелепипеда и последующем выполнении для каждой сетки одной проверки на пересечение луча со сферой (или параллелепипедом). Тогда мы можем сказать, что объект поражен, если луч пересекается с его ограничивающим объемом. Это достаточно хорошая аппроксимация; если требуется большая точность, мы можем использовать проверку пересечения луча со сферой или параллелепипедом для того, чтобы отбросить те объекты, которые явно не задеты, а затем выполнить дополнительные более точные проверки для тех объектов сцены, чьи ограничивающие объемы пересекает луч.
Библиотека D3DX предоставляет функции для вычисления ограничивающей сферы и ограничивающего параллелепипеда сетки. В качестве входных данных функции получают массив вершин сетки для которой вычисляется ограничивающая сфера или ограничивающий параллелепипед.
Функции достаточно гибкие и могут работать с различными форматами вершин.
HRESULT D3DXComputeBoundingSphere( LPD3DXVECTOR3 pFirstPosition, DWORD NumVertices, DWORD dwStride, D3DXVECTOR3* pCenter, FLOAT* pRadius );
pFirstPosition — Указатель на описывающий местоположение вектор в структуре данных первой вершины из массива вершин.
NumVertices — Количество вершин в массиве вершин.
dwStride — Размер данных каждой вершины в байтах. Эти сведения необходимы потому что в структуре данных вершины может храниться дополнительная информация, такая как вектор нормали или координаты текстуры, которая не требуется для вычисления ограничивающей сферы, и функция должна знать, сколько байт следует пропустить, чтобы перейти к данным местоположения следующей вершины.
pCenter — Возвращает координаты центра ограничивающей сферы.
pRadius — Возвращает радиус ограничивающей сферы.
HRESULT D3DXComputeBoundingBox( LPD3DXVECTOR3 pFirstPosition, DWORD NumVertices, DWORD dwStride, D3DXVECTOR3* pMin, D3DXVECTOR3* pMax );
Первые три параметра те же самые, что и первые три параметра в функции D3DXComputeBoundingSphere. Последние два параметра используются для возврата координат двух углов ограничивающего параллелепипеда.